Prevendo a volatilidade do mercado com modelos de IA

Preveja a volatilidade do mercado e ganhe um prêmio de até $25.000,00.

Como um dos principais formadores de mercado eletrônico global, a Optiver está dedicada a melhorar continuamente os mercados financeiros, criando melhor acesso e preços para opções, ETFs, ações à vista, títulos e moedas estrangeiras em várias bolsas ao redor do mundo. As equipes da Optiver passam inúmeras horas construindo modelos sofisticados que preveem a volatilidade e geram continuamente preços de opções mais justos para os investidores finais. No entanto, um algoritmo de precificação líder na indústria nunca pode parar de evoluir, e não há lugar melhor do que o Kaggle para ajudar a Optiver a levar seu modelo para o próximo nível.

Agradecimentos

Primeiramente, gostaria de agradecer à Optiver pelo incentivo financeiro e pela oportunidade de lidar com dados do mundo real e adquirir insights inestimáveis sobre volatilidade e estrutura do mercado financeiro. Foi uma experiência desafiadora e gratificante.

Introdução

A volatilidade é um dos termos mais proeminentes que você ouvirá em qualquer sala de negociação – e por boas razões. Nos mercados financeiros, a volatilidade captura a quantidade de flutuação nos preços. Alta volatilidade está associada a períodos de turbulência no mercado e a grandes oscilações de preços, enquanto baixa volatilidade descreve mercados mais calmos e tranquilos. Para empresas de negociação como a Optiver, prever com precisão a volatilidade é essencial para a negociação de opções, cujo preço está diretamente relacionado à volatilidade do produto subjacente.

Nesta competição, você construirá modelos que preveem a volatilidade de curto prazo para centenas de ações em diferentes setores. Você terá centenas de milhões de linhas de dados financeiros altamente granulares à sua disposição, com os quais você projetará seu modelo de previsão de volatilidade em períodos de 10 minutos. Os modelos são avaliados em relação aos dados reais do mercado coletados no período de avaliação de três meses após o treinamento.

Através desta competição, você ganhará insights inestimáveis sobre volatilidade e estrutura do mercado financeiro. Você também terá uma melhor compreensão dos tipos de problemas de ciência de dados que a Optiver enfrentou por décadas. Estamos ansiosos para ver as abordagens criativas que a comunidade Kaggle aplicará a este desafio de negociação cada vez mais complexo, mas emocionante.

Metodologia

Descrição dos Dados

Este conjunto de dados contém informações do mercado de ações relevantes para a execução prática de negociações nos mercados financeiros. Em particular, inclui instantâneos do livro de ordens e negociações executadas. Com uma resolução de um segundo, ele oferece uma visão exclusiva e detalhada da microestrutura dos mercados financeiros modernos.

Esta é uma competição onde apenas as primeiras linhas do conjunto de teste estão disponíveis para download. As linhas visíveis têm o objetivo de ilustrar o formato e a estrutura de pastas do conjunto de teste oculto. O restante estará disponível apenas no seu notebook quando ele for submetido. O conjunto de teste oculto contém dados que podem ser usados para construir características para prever cerca de 150.000 valores-alvo. Carregar todo o conjunto de dados exigirá pouco mais de 3 GB de memória, segundo nossa estimativa. Para mais informações sobre os dados entre neste link

Modelo

Random Search foi usado para otimizar os hiperparametros do algoritmo LightGBM. Dividindo o dataset de treinamento em 3 kfolds, foi aplicada validação cruzada para mitigar overfitting do modelo na etapa de treinamento.

Utilizando o voting, uma técnica de ensemble learning, foi construido um modelo robusto a partir de ajustes nas configurações dos hiperparâmetros dos modelos.

modelo1 = lgbm.LGBMRegressor(
                  colsample_bytree=0.1, max_bin=140, max_depth=6,
                  min_child_samples=360, min_child_weight=10.0, n_estimators=1260,
                  n_jobs=-1, num_leaves=80, objective='regression', reg_alpha=0.01,
                  reg_lambda=0.01, subsample=0.01,
                  random_state=2025
                  )

modelo2 = lgbm.LGBMRegressor(
                  colsample_bytree=0.1, max_bin=140, max_depth=12,
                  min_child_samples=360, min_child_weight=10.0, n_estimators=1260,
                  n_jobs=-1, num_leaves=50, objective='regression', reg_alpha=0.01,
                  reg_lambda=0.01, subsample=0.01,
                  random_state=234
                  )

modelo3 = lgbm.LGBMRegressor(
                  colsample_bytree=0.1, max_bin=140, max_depth=4,
                  min_child_samples=360, min_child_weight=10.0, n_estimators=1260,
                  n_jobs=-1, num_leaves=120, objective='regression', reg_alpha=0.01,
                  reg_lambda=0.01, subsample=0.01,
                  random_state=189
                  )


ensemble_voting = VotingRegressor(
    [
        ('model1', modelo1),
        ('model2', modelo2),
        ('model3', modelo3)
    ], weights = [3.0, 4.0, 5.0], verbose=False
).fit(X_train, y_train)

Observação: Os pesos atribuídos aos modelos foram definidos arbitrariamente, utilizando os lados de um triângulo pitagórico como referência.

A figura abaixo, ilustra o modelo.

Métrica de Avaliação

O Root Mean Squared Percentage Error (RMSPE) é uma métrica usada para avaliar a precisão de previsões em relação a valores reais, particularmente em problemas de regressão. Ele mede o erro percentual médio em uma escala quadrática, dando maior peso a erros maiores. Sua fórmula é:

\[\text{RMSPE} = \sqrt{\frac{1}{n} \sum_{i=1}^n \left( \frac{y_i - \hat{y}_i}{y_i} \right)^2}\]

Componentes

• $y_i$: Valor real para a instância $i$.
• $\hat{y}_i$: Valor previsto para a instância $i$.
• $n$: Número total de observações.

Interpretação

1. Escala percentual:
   • O resultado é um valor positivo em forma de percentual. Por exemplo, um RMSPE de 10% significa que, em média, as previsões diferem 10% dos valores reais.
2. Sensibilidade a erros maiores:
   • Como os erros são elevados ao quadrado, valores discrepantes (outliers) têm maior influência no RMSPE, tornando-o sensível a erros extremos.
3. Menor é melhor:
   • Um RMSPE mais baixo indica que o modelo está fazendo previsões mais precisas, enquanto um RMSPE elevado sugere erros maiores nas previsões.
4. Casos específicos:
   • Valores reais próximos de zero podem causar problemas, pois o erro percentual se torna muito grande ($\frac{1}{y_i}$ cresce significativamente)

Exemplo com preço de opção:

A métrica RMSPE é útil para avaliar a precisão de modelos de regressão, especialmente em casos onde os valores reais têm diferentes magnitudes e é importante medir o erro relativo. Um exemplo prático é prever o preço de uma opção financeira.

---

Cenário:

Um modelo é usado para prever o preço de uma opção com base em dados históricos e características do mercado. Suponha que temos os seguintes valores reais ($y_i$) e previstos ($\hat{y}_i$):

Opção	Preço Real ($y_i$)	Preço Previsto ($\hat{y}_i$)
A	$50	$48
B	$20	$25
C	$100	$90

---

Cálculo do RMSPE:

A fórmula do RMSPE é:
\(\text{RMSPE} = \sqrt{\frac{1}{n} \sum_{i=1}^n \left( \frac{y_i - \hat{y}_i}{y_i} \right)^2}\)

1. Erros relativos ao quadrado:
   • Para a Opção A: $\left( \frac{50 - 48}{50} \right)^2 = 0.0016$
   • Para a Opção B: $\left( \frac{20 - 25}{20} \right)^2 = 0.0625$
   • Para a Opção C: $\left( \frac{100 - 90}{100} \right)^2 = 0.01$

2. Média dos erros relativos ao quadrado: \(\frac{0.0016 + 0.0625 + 0.01}{3} = 0.0247\)

3. Raiz quadrada: \(\text{RMSPE} = \sqrt{0.0247} \approx 0.1572 \, (\text{ou } 15.72\%)\)

---

Interpretação:

O RMSPE de $15.72\%$ indica que, em média, as previsões do modelo diferem dos preços reais em cerca de $15.72\%$.

• Para preços altos, como na Opção C, a diferença absoluta ($10) é mais tolerável em termos percentuais.
• Já para preços baixos, como na Opção B, o impacto de uma diferença de $5 é mais significativo.

No notebook, a métrica RMSPE foi implementada da forma a seguir:

def rmspe(y_true, y_pred):
    assert len(y_true) == len(y_pred)
    return np.sqrt(np.mean(
            np.square(((y_true - y_pred) / y_true))
        ))

Resultado

O modelo ensemble utilizando LightGBM apresentou os melhores resultados, alcançando um RMSPE de 0.28978 nos dados da leaderboard privada.

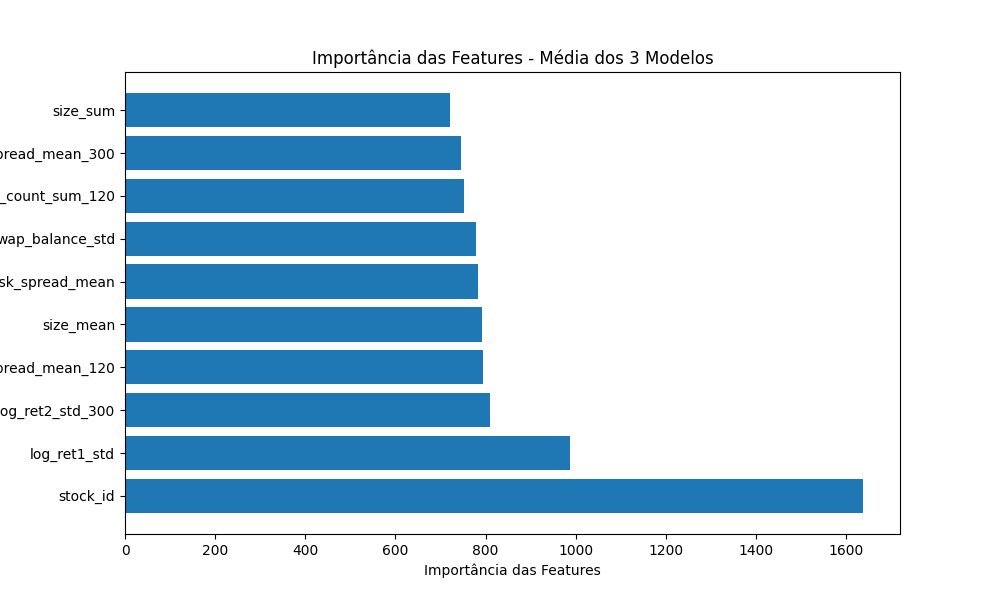
Grafico da feature importances média dos modelos:

A variável stock_id destacou-se como a mais importante. Outras variáveis, como log_ret1_std e log_ret2_std_300, também mostraram alta importância. Fatores relacionados a volumes de negociação e spreads, como spread_mean_120, size_mean e risk_spread_mean, também tiveram pesos notáveis.

Conclusão

Um RMSPE de 0.28978 (ou 28.978%) sugere que o modelo apresenta um erro percentual médio razoável, mas ainda há espaço para melhoria. Isso significa que, em média, as previsões do modelo diferem dos valores reais em aproximadamente 29%.

A variável stock_id é significativamente mais importante que as demais. Isso sugere que as diferenças entre as ações (identificadas pelo ID) são um dos fatores mais críticos na previsão do modelo. Essa dominância pode indicar que o comportamento específico de cada ação (talvez relacionado a características individuais como liquidez, volatilidade, ou setor) desempenha um papel central.

Variáveis como log_ret1_std e log_ret2_std_300 também apresentam uma importância elevada, sugerindo que métricas de retorno logarítmico e sua variabilidade são fundamentais na previsão. Isso indica que a volatilidade ou dispersão dos retornos em diferentes períodos pode ter um impacto relevante na variável-alvo.

Variáveis como spread_mean_120, size_mean, e risk_spread_mean também possuem pesos notáveis, indicando que fatores relacionados a volumes de negociação e spreads desempenham um papel importante no modelo. Esses fatores geralmente estão associados à liquidez e eficiência do mercado.

Algumas variáveis no gráfico apresentam menor importância relativa, como spread_mean_300 e size_sum. Apesar disso, podem ter impacto combinado com outras variáveis ou capturar padrões específicos.

O domínio de poucas variáveis-chave, como stock_id, pode indicar a necessidade de explorar mais interações ou criar variáveis derivadas para capturar informações não lineares ou dependências mais complexas. Focar na feature engineering relacionada às variáveis mais importantes pode ajudar a reduzir ainda mais o RMSPE.

Avaliar se o modelo está capturando bem a relação entre as variáveis mais importantes e a variável alvo. Testar abordagens diferentes, como agrupamento de ações (stock_id) por características similares, para simplificar a estrutura do modelo. Podem contribuir para reduzir o RMSPE.

Citação

Autor: Andrew Meyer, BerniceOptiver, CameronOptiver, IXAGPOPU, Jiashen Liu, Matteo Pietrobon (Optiver), OptiverMerle, Sohier Dane, and Stefan Vallentine. (2021). Title: Optiver Realized Volatility Prediction. Retrieved December 29, 2024 from https://kaggle.com/competitions/optiver-realized-volatility-prediction.

Notebook leaderboard private: https://www.kaggle.com/code/jeffersonrafael/jefferson-version-feature-engineering-lightgbm

---